In this post, I will cover the classic exercise of calculating the electric field inside a uniformly charged sphere with a charge density \(\rho\). Subsequently, this will allow us to calculate the electric field value at any point within the sphere. Let’s start by presenting the problem and setting up the framework to solve it.
For the purpose of this exercise, you may think of the uniformly charged sphere as a spherical metal conductor that is frozen in time at the exact unlikely instant where all of the free electrons are distributed evenly across all the atoms.
Now, taking advantage of the unique spherical symmetry of the charge distribution, we setup within the electric field a Gaussian surface (radius \(r\)) in such a way it will be concentric with it. The electric field at the Gaussian surface is then radial.
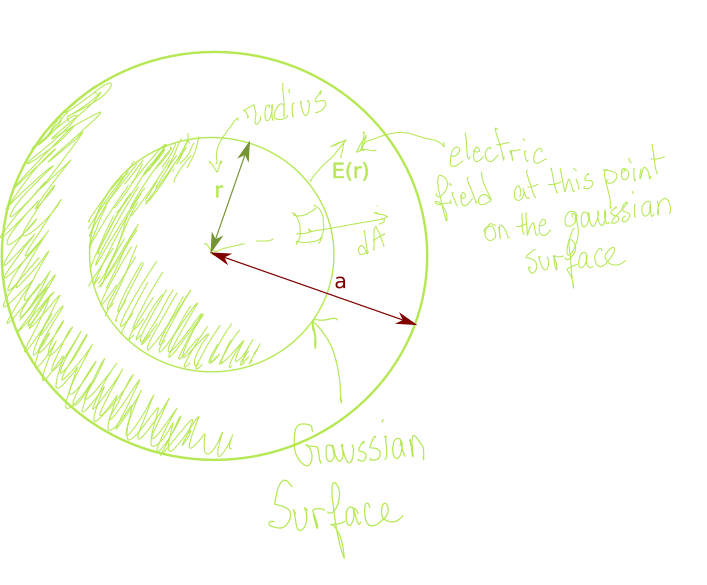
Let’s calculate the electric flux through the gaussian surface:
\[\Phi_E = \oint_{surface} \vec{E}\cdot d\vec{a}\]Because, \(d\vec{a}\) is always aligned with \(\vec{E}\) we can drop the dot product:
\[\Phi_E = \oint_{surface} \vec{E}\cdot d\vec{a} = 4\pi r^2 E(r)\]Notice how we are only interested in the value of \(E\) which only depends on the radius given it’s concentric nature. The field diminishes as the radius increases. Moreover, it remains the same across the surface for a specific radius. Let’s apply the powerful Gauss’s law now which states:
\[\Phi_E = \oint_{surface} \vec{E}\cdot d\vec{a} = \frac{Q_{enc}}{\epsilon_0}\]where \(\epsilon_0\) is the permitivity in vacuum and \(Q_{enc}\) is the total charged enclosed within a surface 🤯.
It’s easy to calculate \(Q_{enc}\):
\[Q_{enc} = \frac{4}{3} \pi r^3 \rho\]Putting everything together:
\[\Phi_E = 4\pi r^2 E(r) = \frac{Q_{enc}}{\epsilon_0} = \frac{4 \pi r^3 \rho}{3 \epsilon_0}\] \[E(r) = \frac{r\rho}{3 \epsilon_0}\]We know that:
\[\rho = \frac{3 q}{4\pi a^3}\]The density charge \(\rho\) is equal to the total charge \(q\) devided by the volume \(4\pi a^3\) of the charge distribution. So the final answer becomes:
\[E(r) = \frac{r q}{4\pi a^3}\]